Runda Figurer

Runda geometriska figurer innehåller krökta linjer. En geometrisk figur med konstant radie runt en punkt är en cirkel. En cirkelsektor och cirkelsegment är exempel på delar av en cirkel. En geometrisk figur med en varierande radie runt en punkt kan vara en ellips.

För cirklar finns det ett samband mellan dess omkrets och diameter. Ration mellan dess omkrets och diameter har beteckningen π (grekiska bokstaven pi). $$\pi = \frac{omkrets}{diameter}$$ π är ett så kallat irrationellt tal, dvs det har ett oändligt antal decimaler. De första siffrorna i π är 3.14159265358979..., men när man räknar med π brukar det räcka med 3.14.

π används ofta när man räknar ut olika egenskaper på cirkulära figurer. π kan även kallas Arkimedes konstant eller Ludolphs tal.

Cirkel

En cirkel begränsas av en krökt linje som i alla positioner ligger på ett konstant avstånd (radie) från en punkt (cirkelns centrum).

För en cirkel finns ett antal definerade termer. Några av dessa kan ses i figurna nedan med förklaringar i texten under.


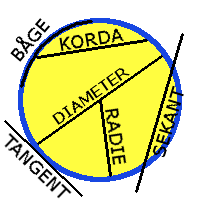
Radie: En rät linje som går från sidan (periferin) till cirkelns centrum (mittpunkt eller origo).

Diameter: En rät linje som går från sida till sida och går igenom cirkelns mittpunkt.

En cirkels diameter har således samma längd som två radier. $$diameter = 2 \times radie$$
Korda: En rät linje från sida till sida.
En korda delar cirkeln i två segment. Kordans längd kan räknas ut enligt:$$s=2 \sqrt{h(2r-h)}$$ Kordans höjd i av det yttre segmentet kan räknas ut enligt:$$h=r- \frac{\sqrt{4r^2-s^2}}{2}$$ För att räkna fram kordans längd behöver man dess höjd och tvärtom.

Sekant: En rät linje som skär en cirkel.
Den del av sekanten som ligger i cirkeln är en korda.

Tangent: En rät linje som tangerar (ligger precis på kanten utan att skära den) en cirkel.

Båge: Del av sidan på cirkeln.
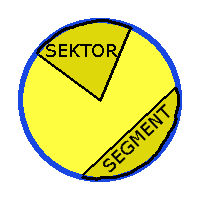
Vinkeln i mitten av cirkeln som bågen sträcker sig runt kallas medelpunktsvinkeln. Bågens längd räknas ut genom att multiplicera medelpunktsvinkelns andel av ett helt varv, med den totala omkretsen på cirkeln enligt:$$b=\frac{\varphi}{360^{\circ}} \cdot \pi \cdot d$$ Sektor: En cirkelsektor är en del av cirkeln som begränsas av en båge och två radier.

Segment: Ett cirkelsegment är en del av cirkeln som begränsas av en båge och en korda.

Cirkelns Ekvation

Matematiskt kan en cirkel beskrivas som samtliga punkter som uppfyller: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$ där (x, y) är en godtycklig punkt på cirkeln, (x0, y0) är cirkelns mittpunkt och r är cirkelns radie.

För en cirkel med mittpunkten i origo blir ekvationen: $$ x^2 + y^2 = r^2 $$
En cirkel kan även beskrivas på parameterform: $$ x = x_0 + r \cdot \cos{t} $$ $$ y = y_0 + r \cdot \sin{t}$$ där (x, y) är en godtycklig punkt på cirkeln, (x0, y0) är cirkelns mittpunkt, r är cirkelns radie och t varierar inom intervallet -π ≤ t ≤ π (eller -180° ≤ t ≤ 180°)

För en cirkel med mittpunkten i origo blir parameterformen: $$ x = r \cdot \cos{t} $$ $$ y = r \cdot \sin{t}$$

Cirkelsektor

En cirkelsektor är en del av en cirkel och begränsas av två radier och en cirkelbåge.

Kvartscirkel, halvcirkel och trekvartscirkel är några specialfall av en cirkelsektor.

Cirkelsegment

Ett cirkelsegment är en del av en cirkeln som avgränsas av en rak linje som skär igenom cirkeln.

Ellips

En ellips begränsas av de punkter där summan av avstånden till två punkter (brännpunkter) är konstant.

En ellips är även ett resultat av ett plant diagonalt snitt genom en cirkulär kon (kägelsnitt) där snittytan får formen av en ellips.

Ellipsens stora axel (där brännpunkterna F1 och F2 ligger) kallas storaxel. Axeln vinkelrätt mot storaxeln som går igenom mittpunkten kallas lillaxel.

Halva ellipsens utbredning på storaxeln betecknas a och halva utbredningen på lillaxeln betecknas b. Avståndet från mittpunkten till en av brännpunkterna betecknas c. De två brännpunkterna ligger på samma avstånd från mittpunkten.

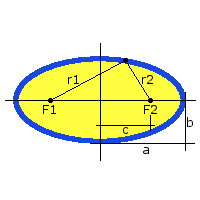
Samtliga punkter på ellipsen ligger där summan av avstånden till brännpunkterna har ett konstant värde: $$r1+r2=2 \cdot a$$ Förhållandet mellan avståndet från mittpunkt till en brännpunkt (c enligt ovan) och halva utbredningen på storaxeln (a enligt ovan) kallas ellipsens excentricitet: $$e=\frac{c}{a} $$ Excentriciteten kan anta värden mellan 0 och 1 (men inte 0 eller 1). För värdet 0 blir det en cirkel då brännpunkterna sammanfallar med mittpunkten. Ju större excentricitet desto mer avlång blir ellipsen.

Ellipsens Ekvation

Matematiskt kan en ellips beskrivas som samtliga punkter som uppfyller: $$ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 $$ där (x, y) är en godtycklig punkt på ellipsen, (x0, y0) är ellipsens mittpunkt, a är halva storaxeln och b är halva lillaxeln.

För en ellips med mittpunkten i origo blir ekvationen: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
En ellips kan även beskrivas på parameterform: $$ x = x_0 + a \cdot \cos{t} $$ $$ y = y_0 + b \cdot \sin{t}$$ där (x, y) är en godtycklig punkt på ellipsen, (x0, y0) är ellipsens mittpunkt, a är halva storaxeln, b är halva lillaxeln och t varierar inom intervallet -π ≤ t ≤ π (eller -180° ≤ t ≤ 180°)

För en ellips med mittpunkten i origo blir parameterformen: $$ x = a \cdot \cos{t} $$ $$ y = b \cdot \sin{t}$$

Omkrets

För en cirkel beräknas omkretsen enligt: $$omkrets_{cirkel}=\pi \cdot d$$ där d är diametern.


För en cirkelsektor beräknas omkretsen enligt: $$omkrets_{cirkelsektor}=b + 2r$$ där b är bågens längd och r är radien.


För ett cirkelsegment beräknas omkretsen enligt: $$omkrets_{cirkelsegment}=b + s$$ där b är bågens längd och s är kordans längd.


För en ellips kan omkretsen beräknas approximativt enligt: $$omkrets_{ellips} \approx \pi (3(a+b)-\sqrt{(3a+b)(a+3b)})$$ där a är halva storaxeln och b är halva lillaxeln.

Area

För en cirkel beräknas arean enligt: $$area_{cirkel}=\pi \cdot r^2$$ där r är radien.


För en cirkelsektor beräknas arean enligt: $$area_{cirkelsektor}=\frac{\varphi}{360^\circ} \pi \cdot r^2$$ där φ är mittpunktsvinkeln och r är radien.


För ett cirkelsegment beräknas arean enligt: $$area_{cirkelsegment}=\frac{r^2}{2}(\frac{\varphi \cdot \pi}{180^{\circ}} - \sin{\varphi})$$ där φ är mittpunktsvinkeln och r är radien.


För en ellips beräknas arean enligt: $$area_{ellips}=\pi \cdot a \cdot b$$ där a är halva storaxeln och b är halva lillaxeln.