Trianglar (Trigon)

En triangel (trigon, trekant, tresiding eller trehörning) har tre sidor. Namnet triangel kommer ifrån latin (triangulum) och betyder trehörning. Triangeln består av tre räta linjer som var och en skär de andra två linjerna. Skärningspunkterna bildar triangelns hörn.

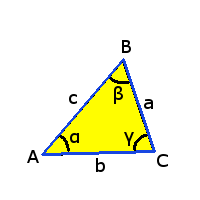Triangelns hörn brukar namnges A, B och C medans sidorna har namnen a, b och c. De inre vinklarna brukar ha beteckningarna α, β och γ (alfa, beta och gamma). Ett hörns motstående sida har samma bokstav, tex sidan b ligger motstående hörnet B. De tre sidorna och de tre vinklarna brukar kallas triangelns element.

Vinkelsumma: Vinkelsumman i en triangel är summan av de inre vinklarna och blir alltid 180 grader. $$\alpha \times \beta \times \gamma=180 ^{\circ}$$
Bas och Höjd: Höjden i en triangel är det vinkelräta avståndet från en godtycklig sida av triangeln (basen) till motstående hörn. 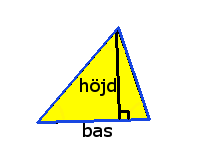I en triangel finns det tre höjder och skärningspunkten mellan dessa kallas ortocentrum.

Liksidig Triangel

En liksidig triangel har alla sidor lika långa.

Likbent Triangel

En likbent triangel har två sidor lika långa.

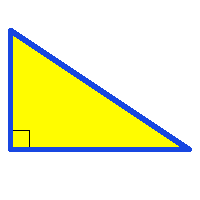
Rätvinklig triangel

En rätvinklig triangel har ett hörn med rät vinkel (90 grader).

Spetsvinklig triangel

En spetsvinklig triangel har alla hörn med spetsig vinkel (mindre än 90 grader).

Trubbvinklig triangel

En trubbvinklig triangel har ett hörn med trubbig vinkel (mer än 90 grader).

Area

För att räkna ut arean på en triangel kan man använda formeln: $$area=\frac{basen \times höjden}{2}$$

Basen på triangeln är en av sidorna. Höjden är det vinkelräta avståndet från basen till motstående hörn.

Herons Formel: Arean kan även räknas ut med herons formel: $$area=\sqrt {s(s-a)(s-b)(s-c)}$$ a, b och c är längderna på sidorna och s är Semiperimetern (=halva omkretsen): $$s=\frac{1}{2}(a+b+c)$$

Areasatsen: Arean kan även räknas ut med areasatsen: $$area=\frac{ab \sin \gamma}{2}=\frac{ac \sin \beta}{2}=\frac{bc \sin \alpha}{2}$$ a, b och c är sidorna och α, β och γ är vinklarna i triangeln.

Höjd

En triangels höjd är det vinkelräta avståndet från en godtycklig sida av triangeln (basen) till motstående hörn.

Längden av respektive höjd kan räknas ut enligt: $$h_{a}=\frac{2}{a}\sqrt{s(s-a)(s-b)(s-c)}$$ $$h_{b}=\frac{2}{b}\sqrt{s(s-a)(s-b)(s-c)}$$ $$h_{c}=\frac{2}{c}\sqrt{s(s-a)(s-b)(s-c)}$$ h är längden på respektive höjd, a, b och c är längderna på sidorna och s är Semiperimetern (=halva omkretsen): $$s=\frac{1}{2}(a+b+c)$$

Bisektris

En triangels bisektris är en rät linje som går från ett hörn till motstående sida och delar hörnets vinkel i två lika delar.

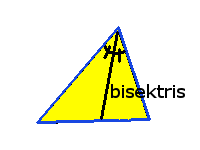
Bisektrissatsen: En bisektris delar motstående sida i samma proportioner som sidorna i triangeln.

$$\frac{x}{y}=\frac{a}{b}$$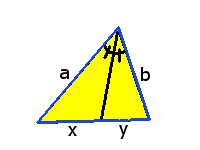

Bisektrisens längd: Längden på respektive bisektris kan räknas ut enligt:

$$d_{a}=\frac{2bc \cos(\frac{\alpha}{2})}{b+c}$$ $$d_{b}=\frac{2ac \cos(\frac{\beta}{2})}{a+c}$$ $$d_{c}=\frac{2ab \cos(\frac{\gamma}{2})}{a+b}$$

Längden kan även räknas ut med:

$$d_{a}=\frac{2\sqrt{bcs(s-a)}}{b+c}$$ $$d_{b}=\frac{2\sqrt{acs(s-b)}}{a+c}$$ $$d_{c}=\frac{2\sqrt{abs(s-c)}}{a+b}$$ d är längden på respektive bisektris, a, b och c är längderna på sidorna, α, β och γ är vinklarna (innan bisektrisen har delat dem) och s är Semiperimetern (=halva omkretsen): $$s=\frac{1}{2}(a+b+c)$$

Median

En triangels median är en rät linje som går från ett hörn till motstående sida och delar den sidan i två lika delar.

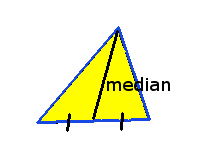
Skärningspunkten mellan triangelns medianer ligger i triangelns tyngdpunkt.

Medianens längd: Längden på respektive median kan räknas ut enligt:

$$m_{a}=\sqrt{\frac{2b^{2}+2c^{2}-a^{2}}{4}}$$ $$m_{b}=\sqrt{\frac{2a^{2}+2c^{2}-b^{2}}{4}}$$ $$m_{c}=\sqrt{\frac{2a^{2}+2b^{2}-c^{2}}{4}}$$ m är längden på respektive median och a, b och c är längderna på sidorna.

Cirklar

Omskriven cirkel: En cirkel som är omskriven runt en triangel (skär alla tre hörnen) har sitt centrum i skärningspunkten från normalerna som utgår från respektive sidas mittpunkt.

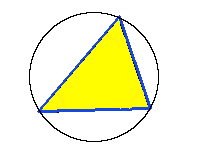
En omskriven cirkel har radien: $$radie=\frac{abc}{4 \sqrt{s(s-a)(s-b)(s-c)}}$$ a, b och c är längderna på sidorna och s är Semiperimetern (=halva omkretsen): $$s=\frac{1}{2}(a+b+c)$$

Inskriven cirkel: En cirkel som är inskriven i en triangel (tangerar all tre sidor) har sitt centrum i skärningspunkten från triangelns bisektriser.

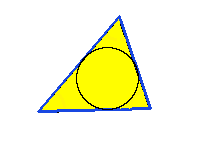
En inskriven cirkel har radien: $$radie=\sqrt{\frac{(s-a)(s-b)(s-c)}{s}}$$ a, b och c är längderna på sidorna och s är Semiperimetern (=halva omkretsen): $$s=\frac{1}{2}(a+b+c)$$

Vidskriven cirkel: En cirkel som är vidskriven en triangel (tangerar en sida och förlängningarna av de två andra sidorna). En triangel har tre stycken vidskrivna cirklar, en för varje av triangelns sidor.

De tre vidskrivna cirklarna har radierna: $$radie_a=\sqrt{\frac{s(s-b)(s-c)}{s-a}}$$ $$radie_b=\sqrt{\frac{s(s-a)(s-c)}{s-b}}$$ $$radie_c=\sqrt{\frac{s(s-a)(s-b)}{s-c}}$$ radierna a, b, och c är radierna för de vidskrivna cirklarna utanför respektive sida, a, b och c är längderna på sidorna och s är Semiperimetern (=halva omkretsen): $$s=\frac{1}{2}(a+b+c)$$

Tyngdpunkt

En triangels tyngdpunkt (masscentrum) ligger i skärningspunkten av triangelns medianer.
Tyngdpunkten ligger på ett avstånd av en tredjedel av höjden vinkelrät från basen eller på en tredjedels avstånd av medianlängden från sidan medianen skär.

Trigonometri

Trigonometri handlar om sambanden mellan sidorna och vinklarna i en triangel.

Sinussatsen: Enligt sinussatsen är kvoterna mellan sinus av ett hörns vinkel och dess motstående sida lika: $$\frac{\sin \alpha}{a}=\frac{\sin \beta }{b}=\frac{\sin \gamma }{c}$$

Cosinussatsen: Enligt cosinussatsen finns det ett samband mellan sidorna och en av vinklarna i en triangel enligt: $$a^{2}=b^{2}+c^{2}-2bc \cos \alpha$$ $$b^{2}=a^{2}+c^{2}-2ac \cos \beta$$ $$c^{2}=a^{2}+b^{2}-2ab \cos \gamma$$

Tangenssatsen: Enligt tangenssatsen finns det ett samband mellan två sidor och deras motstående vinklar enligt: $$\frac{a-b}{a+b}=\frac{\tan (\frac{1}{2}(\alpha - \beta))}{\tan (\frac{1}{2}(\alpha + \beta))}$$

För rätvinkliga trianglar gäller:

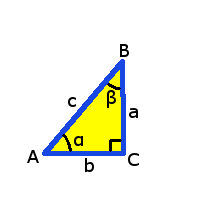
Sinus: Sinus för en vinkel är lika med kvoten av motstående katet genom hypotenusan: $$\sin \alpha=\frac{a}{c}$$

Cosinus: Cosinus för en vinkel är lika med kvoten av närstående katet genom hypotenusan: $$\cos \alpha=\frac{b}{c}$$

Tangens: Tangens för en vinkel är lika med kvoten av motstående katet genom närstående katet: $$\tan \alpha=\frac{a}{b}$$

Pythagoras sats: Enligt pythagoras sats finns det ett samband mellan längderna i en rätvinklig triangel enligt: $$a^{2}+b^{2}=c^{2}$$